量化金融庫是一種軟件包,包含適用于量化投資環境的數學、統計和最近的機器學習模型。它們包含一系列功能,通常為專有功能,用于支持評估、風險管理、組建和優化投資組合。
開發此類庫的金融公司必須在新功能的短期啟用和長期軟件工程考慮之間優先考慮有限的開發者資源。此外,合規、監管和風險管理的約束將對潛在的利潤和損失影響的任何代碼更改提供更嚴格的監督,而 C++標準并行性使舊代碼更具可持續性,并為 GPU 和 CPU 并行性做好準備。
本文展示了如何通過利用CPU和GPU的并行性,使用ISO C++標準重構一個簡單的Black-Scholes模型。同時,它還展示了如何重復使用原始實現中的大部分代碼。對于輔助參考或自行測試實施的代碼,請訪問NVIDIA/accelerated-quant-finance GitHub 庫。這種方法不僅節省了開發者的時間,而且提高了關鍵量化金融庫的性能,是一種低風險且簡單的策略。
我們展示了您應該使用的幾個現代 C++功能,以及如何將現有的 C 或 C++代碼現代化,以利用標準并行性。我們還展示了 C++并行算法如何取代串行for循環來實現代碼并行化。我們還展示了span可以改善對數據的觀察,從而提高代碼的安全性和簡潔性。
借助并行編程應對選擇估值挑戰
選項是具有非線性回報的金融衍生產品。資產組合選擇權的當前價值可能是一個復雜、非線性的多變量函數。在動態市場條件下,資產組合選擇權的行為可能是一項計算密集型任務,因為資產組合選擇權的價值會隨著時間的推移而發生變化。
即使是最簡單的選擇權案例也是如此,因為不同的資產類別的底層會產生對各種市場數據的復雜的依賴關系。了解選擇權組合在各種市場場景下的動態是許多交易活動的關鍵,包括 alpha 生成、風險管理和市場創造。
我們專注于快速評估許多普通選擇權。各種應用程序 (如模擬、回測、策略選擇和優化) 都需要高性能評估。在本例中,我們使用 Black-Scholes 模型評估歐洲選擇權和選擇權。但是,您可以輕松擴展此處討論的方法,應用于其他更復雜的用例。
本文中不會詳細介紹 Black-Scholes 模型的理論細節。我們先從使用 C 語言編寫的給定 Black-Scholes 估值函數開始。這個函數BlackScholesBody計算給定價格、到期日和波動率的選擇權或選擇權的價值。一個名為BlackScholesCPU調用此函數以估值大量選擇 (交易和投資) 的范圍,該范圍包括給定的基準現貨價格和風險免費率。對于每個選擇,我們計算其溢價。
允許貨幣價格或風險免費率波動,考慮不同的基礎資產,或者計算希臘字母,可以進一步擴大我們的選擇范圍。顯然,這個問題具有很大的并行化潛力。
原始基準代碼是相當標準的 C 風格代碼。該函數接受多個數組作為雙精度數據的指針,并包含對所有選項的循環。對于每個選項,Black-Scholes 計算通過調用BlackScholesBody函數。這個函數的詳細信息不重要,但我們選擇在這個函數中包裝計算,以便在我們的第二個示例中重復使用。如果您編寫過任何 C 或 C++代碼,這個函數應該很熟悉。我們在循環中添加了 OpenMP,以便基準代碼至少在多個 CPU 核心上運行,以便進行公平的性能比較。
void BlackScholesCPU( double *CallPrices, double *PutPrices, double spotPrice, double *Strikes, double *Maturities, double RiskFreeRate, double *Volatilities, int optN){ #pragma omp parallel for for (int opt = 0; opt < optN; opt++) { BlackScholesBody( CallPrices[opt], spotPrice, Strikes[opt], Maturities[opt], RiskFreeRate, Volatilities[opt], CALL); BlackScholesBody( PutPrices[opt], spotPrice, Strikes[opt], Maturities[opt], RiskFreeRate, Volatilities[opt], PUT); }} |
雖然這個代碼看起來很熟悉且易于理解,但它有一個重大限制:它是典型的串行代碼。盡管我們已經添加了 OpenMP 宏以實現代碼線程化,但循環仍然是串行循環,并且并行性是在考慮之后才添加的。這種方法在很多年里都很常見,但最近的編碼實踐發展讓我們能夠輕松地設計并行優先算法。以下是一個并行優先實現示例。
void BlackScholesStdPar( std::span CallPrices, std::span PutPrices, double spotPrice, std::span Strikes, std::span Maturities, double RiskFreeRate, std::span Volatilities){ // Obtain the number of options from the CallPrices array int optN = CallPrices.size(); // This iota will generate the same indices as the original loop auto options = std::views::iota(0, optN); // The for_each algorithm replaces the original for loop std::for_each(std::execution::par_unseq, options.begin(), // The starting index options.end(), // The ending condition [=](int opt) // The lambda function replaces the loop body { BlackScholesBody(CallPrices[opt], spotPrice, Strikes[opt], Maturities[opt], RiskFreeRate, Volatilities[opt], CALL); BlackScholesBody(PutPrices[opt], spotPrice, Strikes[opt], Maturities[opt], RiskFreeRate, Volatilities[opt], PUT); });} |
我們對代碼進行了幾項重要更改,但大部分代碼都封裝在BlackScholesBodyCPU函數不會發生任何變化。操作沒有發生變化,而是通過調用具有并行執行策略的標準算法,而非使用串行循環來應用于數據。
我們希望重點介紹以下幾個特性。
首先,我們不再傳遞 raw 指針,而是傳遞 C++橫向塊。橫向塊是指向內存的視圖,并包含某些便利性,例如可以查詢大小。不同于容器vector例如,span只是顯示內存的視圖,因此您可以改變如何訪問內存,而無需更改容器本身。
其次,原始代碼對選項進行了循環。我們使用了 IotaView 來完成相同的操作,每次我們的算法執行時,它都會從 IotaView 接收一個索引。
第三,我們不再使用循環,而是使用for_each算法。C++標準庫提供了各種算法供選擇,for_each提供了原始循環的便捷替代方案,并需要指定幾個參數:
- 執行策略:
par_unseq向編譯器保證代碼可以并行執行并按任意順序執行,從而實現并行執行和矢量執行。nvc++ 編譯器 可以進一步將此代碼卸載到 GPU。請注意,并行執行不是默認行為,但可以通過執行策略進行啟用。 - 循環范圍的起始和終止值:這些值由
options.begin和options.end分辨率分別為 1024×1024 和 2048×204。 - Lambda 函數:此 lambda 執行原始循環體中指定的任務。我們通過值獲取 lambda 中使用的數據,以確保它可在 GPU 上顯示。
應用到代碼中的所有更改都非常簡單。它們只是更新代碼以在語言中使用現代功能。最初可能會覺得有點不熟悉,但如果您同時查看代碼,您會發現幾乎沒有變化:
void BlackScholesCPU( double *CallPrices, double *PutPrices, double spotPrice, double *Strikes, double *Maturities, double RiskFreeRate, double *Volatilities, int optN){ #pragma omp parallel for for (int opt = 0; opt < optN; opt++) { BlackScholesBody( CallPrices[opt], spotPrice, Strikes[opt], Maturities[opt], RiskFreeRate, Volatilities[opt], CALL); BlackScholesBody( PutPrices[opt], spotPrice, Strikes[opt], Maturities[opt], RiskFreeRate, Volatilities[opt], PUT); }} |
void BlackScholesStdPar( std::span CallPrices, std::span PutPrices, double spotPrice, std::span Strikes, std::span Maturities, double RiskFreeRate, std::span Volatilities){ int optN = CallPrices.size(); auto options = std::views::iota(0, optN); std::for_each( std::execution::par_unseq, options.begin(), options.end(), [=](int opt) { BlackScholesBody(CallPrices[opt], spotPrice, Strikes[opt], Maturities[opt], RiskFreeRate, Volatilities[opt], CALL); BlackScholesBody(PutPrices[opt], spotPrice, Strikes[opt], Maturities[opt], RiskFreeRate, Volatilities[opt], PUT); });} |
代碼中的變化很少,但改造代碼可以帶來顯著的性能提升。重要的是,原始代碼是串行的,后來增加了并行性,而新代碼從一開始就是并行的。由于并行代碼可以始終以串行方式運行,因此基準代碼現在可以在CPU上的并行線程中運行,或者將代碼卸載到GPU,而無需更改代碼。對于圖1中顯示的性能圖表,NVIDIA HPC SDK v23.11用于NVIDIA Grace Hopper 超級芯片。在為CPU構建C++代碼時,使用-stdpar=multicore編譯選項;在構建GPU卸載時,使用-stdpar=gpu編譯選項。
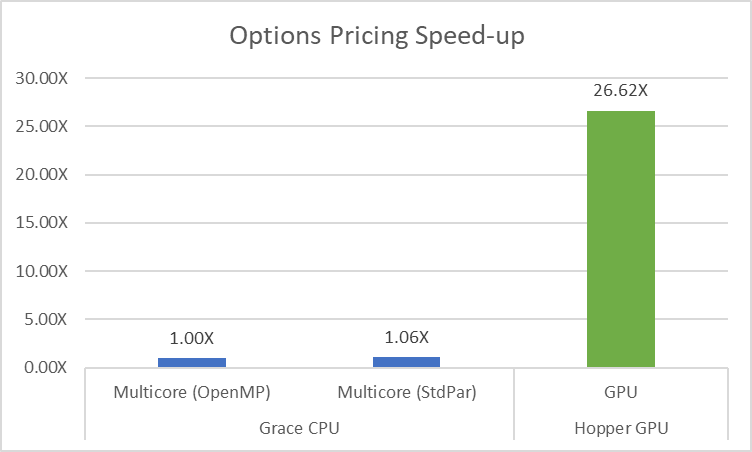
本示例的重要啟示是,默認情況下,應在應用程序中暴露并行性。代碼應從一開始就表達可用的并行性。在同一 CPU 上運行的 ISO C++代碼使用相同的編譯器,運行效果略優于原始代碼,因為編譯器能夠更好地優化純 C++代碼。構建此代碼的速度比構建原始代碼快 26 倍。使用 NVIDIA Hopper GPU,我們得益于大量可用的并行性,在重復使用大量現有代碼的同時完成了所有這些工作。
憑借如此顯著的加速,耗時的投資組合管理工作流程 (如回測和模擬) 變得更加實用。傳統上,這些工作流程依賴于簡化模型 (如維度歸約、Gaussian 分布假設或其他精簡表示選擇) 來減輕計算負擔。現在,這些工作流程可以在更逼真的條件下完成。
采用并行編碼,在量化金融領域實現出色性能
總而言之,本文探討了使用 ISO C++在量化金融領域進行編碼時采用并行先行的方法的變革力量。通過重構現有代碼以利用現代 C++特性 (如 spans 和并行算法),開發者可以在多核 CPU 和 GPU 上無縫釋放并行性潛力。
該示例聚焦于大型選擇權益組合的快速估值,展示了通過 C++標準并行實現的顯著性能提升。原始 OpenMP 代碼與在 CPU 和 GPU 平臺上運行的 ISO C++并行代碼的比較顯示了顯著的加速。這為耗時的選擇權益組合管理工作流程 (如回測和模擬) 開辟了新的可能性。
關鍵要點是顯而易見的:從一開始就使用具有內部并行性的代碼編寫代碼可以實現更高效且更具可擴展性的解決方案。采用現代編碼實踐可以通過編譯器優化性能,尤其是在構建 NVIDIA Hopper GPU 時可以獲得顯著的 26 倍加速。
隨著開發者進入并行編程領域,我們鼓勵他們進行探索和實踐。通過 NVIDIA/accelerated-quant-finance 與 NVIDIA HPC SDK 搭配使用,為深入研究標準并行提供了一條切實可行的途徑。雖然這些資源并非用于生產,但它們卻是寶貴的學習工具,可助力開發者將并行第一原則融入自己的項目中。
量化金融領域的編碼未來在于采用并行性作為基礎原則。通過這樣做,開發者為提升性能、增強可擴展性和導航金融領域技術領域不斷發展的技術環境奠定了基礎。在編碼領域,最佳代碼始終以并行性為先。
?