設計深度網絡以處理其他深度網絡

深度神經網絡（DNN）是從數據中學習函數的首選模型，如圖像分類器或語言模型。近年來，深度模型由于表示數據樣本本身而變得流行起來。例如，可以訓練深度模型來表示圖像、3D 對象或場景，這種方法稱為Implicit Neural Representations（另請參閱 Neural Radiance Fields和Instant NGP)。請繼續閱讀一些對預訓練的深度模型執行操作的示例，這些模型包括作為函數的 DNN 和作為數據的 DNN。

假設您有一個使用隱式神經表示（INR）或神經輻射場（NeRF）表示的 3D 對象數據集。通常，您可能希望“編輯”對象以更改其幾何圖形或修復錯誤和異常。?例如，拆除一個杯子的把手或使所有車輪比 NeRF 重建的車輪更對稱。

不幸的是，使用 INR 和 NeRF 的一個主要挑戰是，它們必須在編輯之前進行渲染。實際上，編輯工具依賴于渲染對象并直接微調 INR 或 NeRF 參數。例如，3D 神經雕塑 (3DNS)：編輯神經符號距離函數直接改變 NeRF 模型的權重而不將其渲染回 3D 空間會更有效。

作為第二個例子，考慮一個經過訓練的圖像分類器。在某些情況下，您可能希望將某些轉換應用于分類器。例如，您可能希望使用在下雪天氣中訓練的分類器，使其對陽光充足的圖像準確無誤。這是一個領域自適應問題的例子。

然而，與傳統的域自適應方法不同，該設置側重于學習將函數（分類器）從一個域映射到另一個域的一般操作，而不是將特定分類器從源域轉移到目標域。

處理其他神經網絡的神經網絡

我們團隊提出的關鍵問題是神經網絡能否學會執行這些操作。我們尋求一種特殊類型的神經網絡“處理器”，可以處理其他神經網絡的權重。

這反過來又提出了一個重要的問題，即如何設計能夠處理其他神經網絡權重的神經網絡。這個問題的答案并沒有那么簡單。

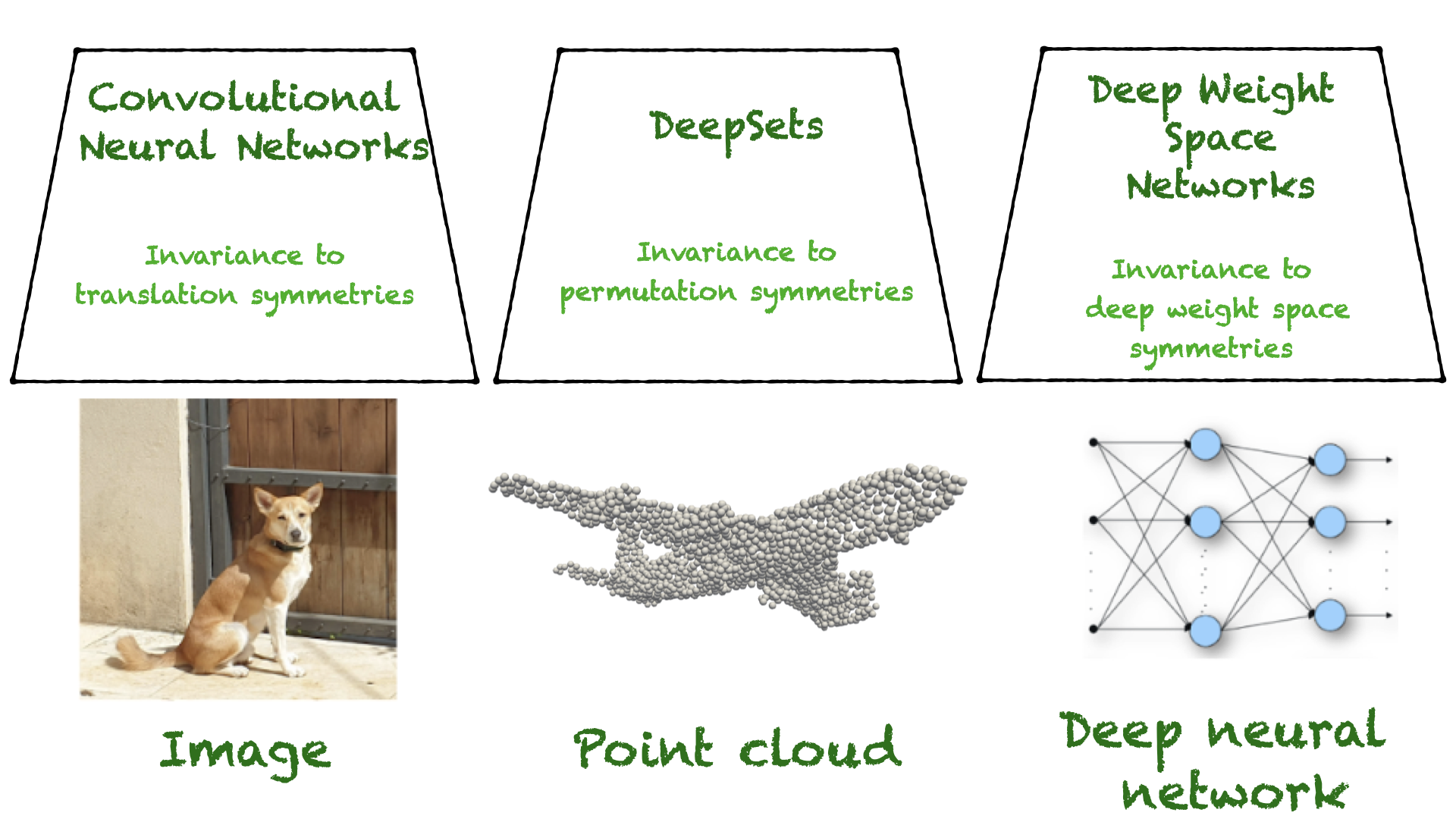
This figure illustrates three deep networks, for three spaces that have invariance properties: Images are invariant to translation, point clouds are invariant to permutations, and neural networks are invariant to deep-weight-space symmetries. Each data type has data-specialized architectures: convolutional neural networks for images and DeepSets for point clouds, and deep-weight-space networks for the third case. — *圖 1。數據專用架構的兩個示例：用于圖像的卷積神經網絡和用于點云的 DeepSets*

以前處理深權重空間的工作

表示深度網絡參數的最簡單方法是將所有權重（和偏差）矢量化為簡單的平面向量。?然后，應用一個全連接網絡，也稱為多層感知器（MLP）。

一些研究已經嘗試了這種方法，并表明這種方法可以預測輸入神經網絡的測試性能。詳情請參見Classifying the Classifier: Dissecting the Weight Space of Neural Networks， Hyper-Representations: Self-Supervised Representation Learning on Neural Network Weights for Model Characteristic Prediction和 Predicting Neural Network Accuracy from Weights。

不幸的是，這種方法有一個主要缺點，因為神經網絡權重的空間具有復雜的結構（下面將更全面地解釋）。將 MLP 應用于所有參數的矢量化版本會忽略該結構，因此會損害泛化能力。這種效果類似于其他類型的結構化輸入，如圖像。這種情況最適用于對輸入圖像的小偏移不敏感的深度網絡。

解決方案是使用卷積神經網絡。它們的設計方式在很大程度上對圖像的變化“視而不見”，因此，可以推廣到訓練中沒有觀察到的新變化。

在這里，我們希望設計遵循相同想法的深層架構，但我們希望設計對模型權重的其他轉換不敏感的架構，而不是考慮圖像偏移，如下所述。

具體來說，神經網絡的一個關鍵結構特性是，它們的權重可以被排列，同時它們仍然計算相同的函數。圖 2 說明了這種現象。當將全連通網絡應用于矢量化權重時，忽略了這一重要特性。

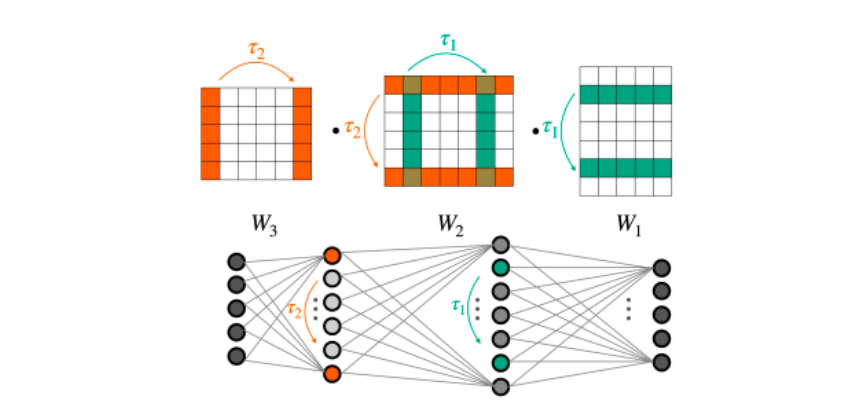
The figure illustrates the weight symmetries of a multilayer perceptron (MLP) with two hidden layers. Changing the order of neurons in internal layers preserves the function represented by the MLP. — *圖 2:具有兩個隱藏層（底部）的多層感知器（MLP）的權重對稱性（頂部）。改變內層神經元的順序可以保留 MLP 所代表的功能*

不幸的是，一個在平面向量上運行的全連接網絡認為所有這些等價表示都是不同的。這使得網絡更難在所有此類（等效）表示中進行泛化。

對稱性和等變體系結構簡介

幸運的是，前面的 MLP 限制已經在機器學習的一個子領域進行了廣泛的研究，即幾何深度學習（GDL）。GDL 是關于學習對象，同時對這些對象的一組變換保持不變，比如移動圖像或排列集。這組轉換通常被稱為對稱群。

在許多情況下，?學習任務對這些轉換是不變的。例如，查找點云的類應該與點在網絡中的順序無關，因為該順序無關緊要。

在其他情況下，如點云分割，云中的每個點都被分配了一個類，它屬于對象的哪個部分。在這些情況下，如果輸入被排列，輸出點的順序必須以相同的方式改變。這些函數的輸出根據輸入變換進行變換，稱為等變的功能。

更正式地說，對于一組變換 G，函數 L:V→ 如果 W 與群作用交換，則稱為 G-等變，即對于所有 v∈v，G∈G，L（gv）=gL（v）不變的作用

在不變函數和等變函數這兩種情況下，限制假設類都是非常有效的，并且這種對稱感知架構由于其有意義的歸納偏差而提供了幾個優點。例如，它們通常具有更好的樣本復雜性和更少的參數。在實踐中，這些因素導致了明顯更好的概括。

權重空間的對稱性

本節解釋深權重空間的對稱性。有人可能會問這樣一個問題：哪些轉換可以應用于 MLP 的權重，這樣 MLP 表示的底層函數就不會改變？

一種特定類型的轉換，稱為神經元排列，是這里的焦點。直觀地說，當觀察 MLP 的圖形表示時（如圖 2 中的圖），改變某個中間層神經元的順序不會改變函數。此外，可以針對每個內部層獨立地進行重新排序過程。

在更正式的術語中，MLP 可以使用以下方程組來表示：

? $f(x)= x_M, \quad x_{m+1}=\sigma(W_{m+1} x_m +b_{m+1}), \quad x_0=x$

這個重量空間該體系結構的定義為（線性）空間，包含所有矢量化權重和偏差的串聯 $[W_m, b_l]_{ m \in [M],l\in[M]}$ 重要的是，在該設置中，權重空間是（即將定義的）神經網絡的輸入空間。

那么，權重空間的對稱性是什么？對神經元進行重新排序可以被形式化建模為將排列矩陣應用于一層的輸出，并將相同的排列矩陣應用到下一層。形式上，一組新的參數可以由以下方程定義：

$W_1 \rightarrow P^T W_1$

$W_2 \rightarrow W_2P$

新的參數集是不同的，但很容易看出，這樣的轉換不會改變 MLP 表示的函數。這是因為兩個置換矩陣 $P$ 和 $P^T$ ?相互抵消（假設像 ReLU 這樣的元素激活函數）。

更一般地，如前所述，不同的排列可以獨立地應用于 MLP 的每一層。這意味著更多一般的轉換集不會改變底層函數。把這些想象成對稱性重量空間。

$(W_1,\dots,W_M) \rightarrow (P_1^TW_1,P_2^TW_2P_1,\dots,P_{M-1}^TW_{M-1}P_{M-2},W_MP_{M-1})$

在這里 $P_i$ 表示置換矩陣。30 多年前，赫奇特·尼爾森在《前饋網絡權重空間的代數結構》中提到，類似的變換可以應用于 MLP 的偏差。

構建深度權重空間網絡

文獻中的大多數等變體系結構都遵循相同的配方：定義了一個簡單的等變層，體系結構被定義為這些簡單層的組成，它們之間可能存在點非線性。

一個很好的例子是 CNN 架構。在這種情況下，簡單的等變層執行卷積運算，而 CNN 則被定義為多個卷積的組合。DeepSets 和許多 GNN 架構都遵循類似的方法。想要了解更多信息，請參閱 Weisfeiler 和 Leman 的神經網絡：高階圖神經網絡和不變和等變圖網絡。

當手頭的任務是不變的時，可以使用 MLP 在等變層的頂部添加一個不變層，如圖 3 所示。

The figure illustrates a typical equivariant architecture. It is composed of several simple equivariant layers, followed by an invariant layer and finally a fully connected layer. — *圖 3。一種典型的等變體系結構，由幾個簡單的等變層組成，然后是一個不變層和一個完全連接層*

我們在論文 Equivariant Architectures for Learning in Deep Weight Spaces 中遵循這個配方，我們的主要目標是為上面定義的權重空間對稱性識別簡單但有效的等變層。不幸的是，刻畫一般等變函數的空間可能具有挑戰性。與之前的一些研究一樣（例如 Deep Models of Interactions Across Sets），我們的目標是刻畫所有線性的等變層。

我們開發了一種新的方法來表征線性等變層，該方法基于以下觀察結果：權重空間 V 是表示每個權重矩陣 V=?Wi 的更簡單空間的級聯。（為簡潔起見，省略了偏差術語）。

這一觀察結果很重要，因為它可以寫入任何線性層 $L:V \rightarrow V$ 作為塊矩陣，其第（i，j）個塊是介于 $W_j$ ?和 $W_i$ ??? $L_{ij} : W_j \rightarrow W_i$ .該塊結構如圖 4 所示。

但我們如何才能找到 $L_{ij}$ ? 我們的論文列出了所有可能的情況，并表明其中一些層已經在以前的工作中得到了表征。例如， $L_{ii}$ ??對于內層，其特征在于 Deep Models of Interactions Across Sets。

值得注意的是，在這種情況下，最一般的等變線性層是對只使用四個參數的眾所周知的深集層的推廣。對于其他層，我們提出了基于簡單等變操作的參數化，如池化、廣播和小的全連接層，并表明它們可以表示所有線性等變層。

圖 4 顯示了 L 的結構，它是特定權重空間之間的塊矩陣。每種顏色代表不同類型的圖層。 $L_{ii}$ 每個塊將一個特定的權重矩陣映射到另一個權重矩陣。這種映射是以一種依賴于權重矩陣在網絡中的位置的方式參數化的。

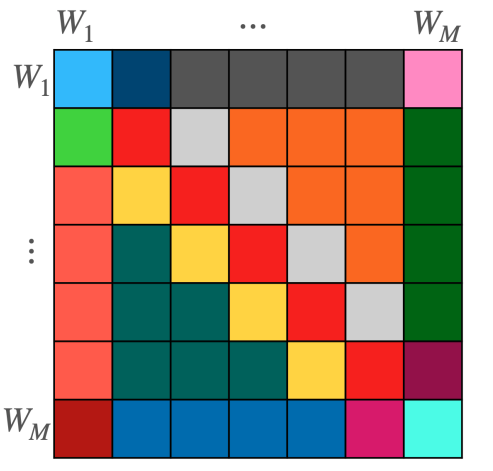
The figure shows colored squares within a larger square, illustrating the block structure of the proposed linear equivariant layer. Each block maps a specific weight matrix to another weight matrix. This mapping is parameterized in a way that relies on the positions of the weight matrices in the network. — *圖 4。所提出的線性等變層的塊結構*

該層是通過獨立計算每個塊，然后對每行的結果求和來實現的。我們的論文涵蓋了一些額外的技術細節，比如處理偏差項和支持多個輸入和輸出特性。

我們將這些層稱為深重空間層（DWS 層），并將由它們構建的網絡稱為深重量空間網絡（DWSNets）。我們在這里關注的是將 MLP 作為輸入的 DWSNets。有關 CNNs 和變壓器擴展的更多詳細信息，請參閱附錄 H 中的Equivariant Architectures for Learning in Deep Weight Spaces。

深權空間網絡的表現力

將我們的假設類限制為簡單的等變函數的組合可能會無意中削弱等變網絡的表達能力。這已經在上面引用的圖神經網絡文獻中得到了廣泛的研究。我們的論文表明 DWSNets 可以近似輸入網絡上的前饋操作，這是理解其表達能力的一步。然后，我們證明 DWS 網絡可以近似 MLP 函數空間中定義的某些“性能良好”的函數。

實驗

DWSNets 在兩個任務族中進行評估。首先，采用表示數據的輸入網絡，如 INR。其次，采用表示標準 I/O 映射（如圖像分類）的輸入網絡。

實驗 1:INR 分類

此設置根據 INR 所代表的圖像對其進行分類。具體來說，它涉及訓練 INR 來代表 MNIST 和時尚 MNIST 的圖像。任務是讓 DWSNet 識別圖像內容，如 MNIST 中的數字，使用這些 INR 的權重作為輸入。結果表明，我們的 DWSNet 體系結構大大優于其他基線。

方法	MNIST INR	Fashion-MNIST INR
MLP	17.55%+-0.01	19.91%+-0.47
MLP+置換擴充	29.26%+-0.18	22.76%+-0.13
MLP+對齊	58.98%+-0.52	47.79%±1.03
INR2Vec（架構）	23.69%+-0.10	22.33%+-0.41
transformer	26.57%+-0.18	26.97%+-0.33
DWSNets（我們的）	85.71%+-0.57	67.06%+-0.29

表 1。對于 INR 分類，INR 的類別由其所代表的圖像定義（平均測試精度)

重要的是，將 INR 分類到它們所代表的圖像類別明顯比對底層圖像進行分類更具挑戰性。在 MNIST 圖像上訓練的 MLP 可以實現近乎完美的測試精度。然而，接受 MNIST INRs 訓練的 MLP 效果不佳。

實驗 2：INRs 的自我監督學習

這里的目標是將神經網絡（特別是 INRs）嵌入到語義連貫的低維空間中。這是一項重要的任務，因為良好的低維表示對許多下游任務至關重要。

我們的數據由擬合到形式為 a\sin（bx）的正弦波的 INR 組成，其中 a、b 是從區間 0,10 上的均勻分布中采樣的。由于數據由這兩個參數控制，因此密集表示應該提取這個底層結構。

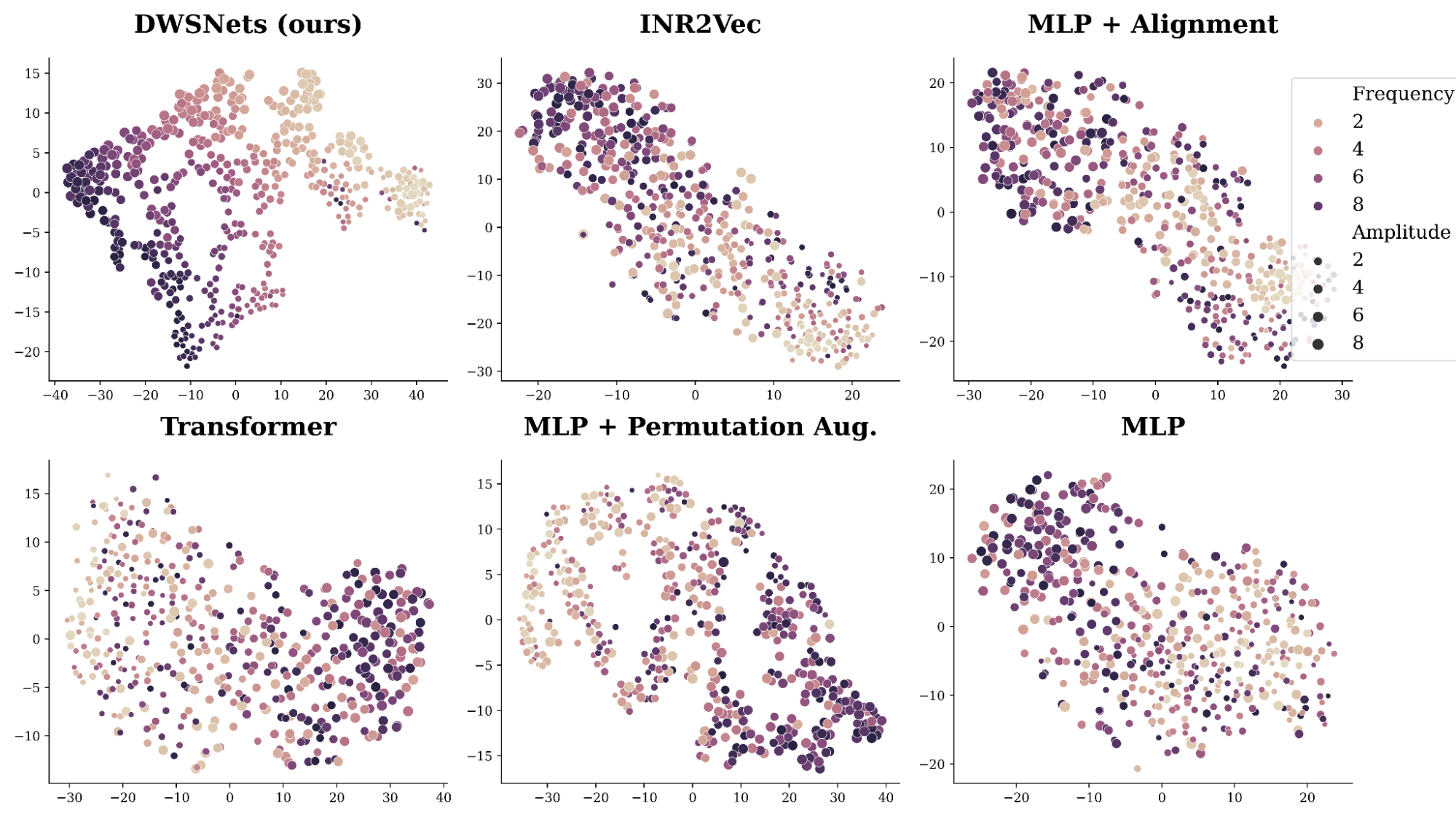
The figure shows 2D TSNE embeddings of input MLPs obtained by training using self-supervision. Each point corresponds to an input MLP that represents a 1D sine wave g(x)=a\sin(bx) with a different amplitude a and frequency b. DWSnets successfully reconstruct the amplitude-frequency space while other methods struggle. — *圖 5。通過使用自我監督的訓練獲得的輸入 MLP 的 TSNE 嵌入*

A.SimCLR 類似的訓練過程和目標被用于通過添加高斯噪聲和隨機掩蔽來從每個 INR 生成隨機視圖。圖 4 顯示了結果空間的 2D TSNE 圖。我們的方法 DWSNet 很好地捕捉到了數據的基本特征，而競爭方法卻舉步維艱。

實驗 3：使預訓練的網絡適應新的領域

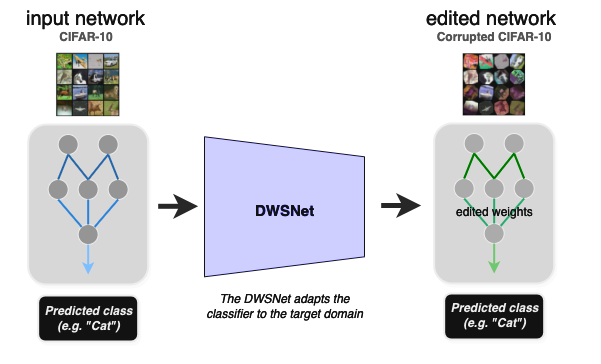
該實驗展示了如何在不進行再訓練的情況下使預訓練的 MLP 適應新的數據分布（零樣本域適應）。給定圖像分類器的輸入權重，任務是將其權重轉換為一組新的權重，該權重在新的圖像分布（目標域）上表現良好。

在測試時，DWSnet 接收一個分類器，并在一次前向傳遞中將其調整為新域。CIFAR10 數據集是源域，其損壞版本是目標域（圖 6）。

Domain adaptation using DWSNets. The DWSNet takes as input a network trained on a source domain (CIFAR10) and its taks is to change the weights such that the output network performs well on a target domain (a corrupted version of CIFAR10). — *圖 6。使用 DWSNets 的域自適應*

結果如表 2 所示。注意，在測試時，模型應該推廣到看不見的圖像分類器，以及看不到的圖像。

方法	CIFAR10->CIFAR10 已損壞
無適應	60.92%+-0.41
MLP	64.33%+-0.36
MLP+置換擴充	64.69%+-0.56
MLP+對齊	67.66%+-0.90
INR2Vec（架構）	65.69%+-0.41
transformer	61.37%+-0.13
DWSNets（我們的）	71.36%+-0.38

表 2。使網絡適應新域。CIFAR-10 腐蝕模型的測試精度

未來研究方向

將學習技術應用于深度權重空間的能力開啟了許多新的研究方向。首先，找到有效的數據擴充方案以在權重空間上提高 DWSNets 的泛化能力是可能的。其次，研究如何為其他類型的輸入架構和層（如跳過連接或規范化層）合并排列對稱性是很自然的。最后，將 DWSNets 擴展到真實世界的應用程序中會很有用，如形狀變形和變形、NeRF 編輯和模型修剪。閱讀 ICML 2023 論文全文，Equivariant Architectures for Learning in Deep Weight Spaces。

有幾篇與此工作密切相關的論文，我們鼓勵感興趣的讀者查閱。首先，論文 Permutation Equivariant Neural Functionals 提供了與此處討論的問題類似的公式，但從不同的角度進行了探討。其次，后續研究 Neural Functional Transformers 建議在線性等變層中使用注意力機制，而非簡單的求和/平均聚合。最后，論文 Neural Networks Are Graphs! Graph Neural Networks for Equivariant Processing of Neural Networks 提出將輸入神經網絡建模為加權圖，并應用 GNN 來處理權重空間。