在科學和工程領域，模擬已經被廣泛用于模擬各種現實問題。人工智能和機器學習的最新發展已經導致使用數據來構建模擬的替代物，但最新的努力集中在將科學定律注入神經網絡上。
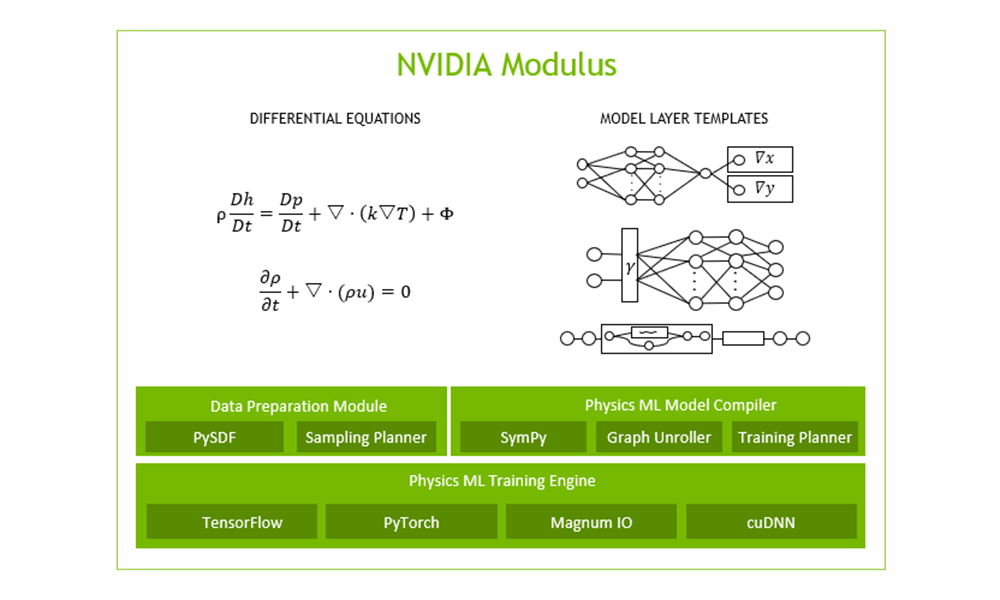
NVIDIA SimNet 是一個基于物理信息神經網絡（ PINN ）的人工智能工具包，可用于解決正向、反向和數據同化問題。希望通過實際應用解決復雜非線性物理問題的工程師、科學家、學生和研究人員可以通過使用 AI 驅動的物理模擬從 SimNet 中獲益。
SimNet 今天應用的一個成功案例是制造和環境空氣控制系統設計優化的自動化。這些使產品設計師能夠在沒有大量領域專業知識的情況下調查任何給定設計的性能。此應用程序使用物理信息神經網絡（ PINNs ）將 2D 噴嘴流的詳細流體動力學解決方案與商業 CAD 軟件耦合。這項工作由邁克爾·艾德爾（ Michael Eidell ）領導，他是 Kinetic Vision 建模與仿真小組的高級工程師。 Kinetic Vision 是一家位于辛辛那提的科技公司，為《財富》 500 強提供服務。他專注于快速為客戶找到見解，并以令人信服的方式傳達這些發現，以幫助客戶通過高效的概念到生產解決方案滿足其復雜的產品和系統開發需求。
Michael 的團隊在 SimNet 和傳統計算物理工具之間觀察到的主要區別因素是，它不依賴網格來離散域，其幾何模塊提供了構建參數化特征的靈活性，例如，邊半徑。代碼在多個 GPU 上的可伸縮性是 Kinetic Vision 團隊成功證明 SimNet 是可行的產品設計工具的另一個因素。
基于仿真的產品設計與優化
作為一家擁有大型產品設計團隊的公司， Kinetic Vision 的工程師通常會對設計性能進行詳細的計算物理評估（例如， FEA 、 CFD ）。這通常包括執行多個設計迭代、生成各種計算網格以及運行第一原理解算器。當考慮到大量的設計變量時，與此過程相關的運行時間和勞動力可能會非常昂貴且時間密集。在某些情況下，可以適當降低模型保真度。但對于涉及復雜流體動力學的問題，必須考慮完整的 Navier-Stokes 方程。
Michael 和他的團隊之前曾探索過使用其他商業溶劑來開發 2D 噴嘴的簡單流體模型。然而，由于多種因素，他們決定使用 SimNet 平臺：
- 該團隊在機器學習領域使用 GPU 的經驗非常豐富。
- 公司內部強烈希望探索 GPU 在基于物理的建模中的使用，以幫助加快產品設計過程以及建模和仿真工作。
- SimNet API 是基于 Python 的，這使得采用和開始對真實世界問題進行原型設計變得更加容易。
SimNet 完全符合團隊的經驗和發展目標。
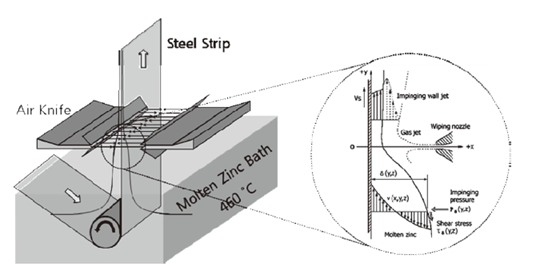
Michael 的團隊開始建立一個 3D 氣刀系統的 2D 模型，模擬鍍鋅過程中使用的熱氣擦拭系統。氣刀是一種亞音速氣體噴嘴，它將氣體排放到附近的鋼帶上，鋼帶已浸沒在熔融鋅中。這種氣體有助于保持鋼帶上鋅的厚度一致，從而對鋼進行鍍鋅（圖 1 ）。
SimNet 入門
使用 SimNet 的幾何模塊，將亞音速氣體噴嘴建模為入口、實心壁和壓力出口，以模擬周圍環境（圖 2 ）。
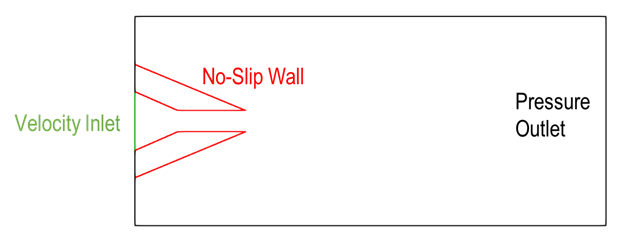
SimNet 中采用的無網格方法仍然需要對感興趣的領域進行適當采樣，以幫助捕獲所有顯著的流動特征。設置問題后，可以使用工具（如 Paraview ）可視化幾何圖形。
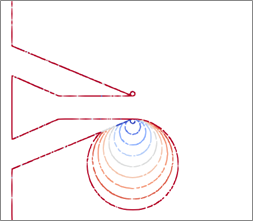
圖 3 比較了 2D 噴嘴問題中可采用的兩種不同批量取樣方法。上部圖像顯示均勻采樣，而下部圖像包括射流潛在核心中的高分辨率區域，其中可能出現一些最大的速度梯度。
探索科恩達效應作為一種控制射流角度的方法，是這一問題的研究重點。 Michael 的團隊通過在噴嘴后緣添加半徑來探索這一點。噴嘴的上后緣具有固定半徑，而噴嘴的下后緣具有變化。圖 4 顯示了在下后緣上探索的一些離散半徑值的簡單描述。
最終培訓的 PINN 與 Solidworks 結合，以幫助演示產品設計師如何在設計氣刀時使用培訓過的模型。簡單矩形氣刀的 CAD 模型是在考慮現有產品的情況下生成的。
設計優化運行
在圖 5 中培訓了 PINN 并開發了 CAD 模型之后，就可以開始與 Solidworks 進行耦合了。圖 6 實際顯示了改變較低的后緣半徑如何為設計提供實時反饋，以確定產生的射流角度。
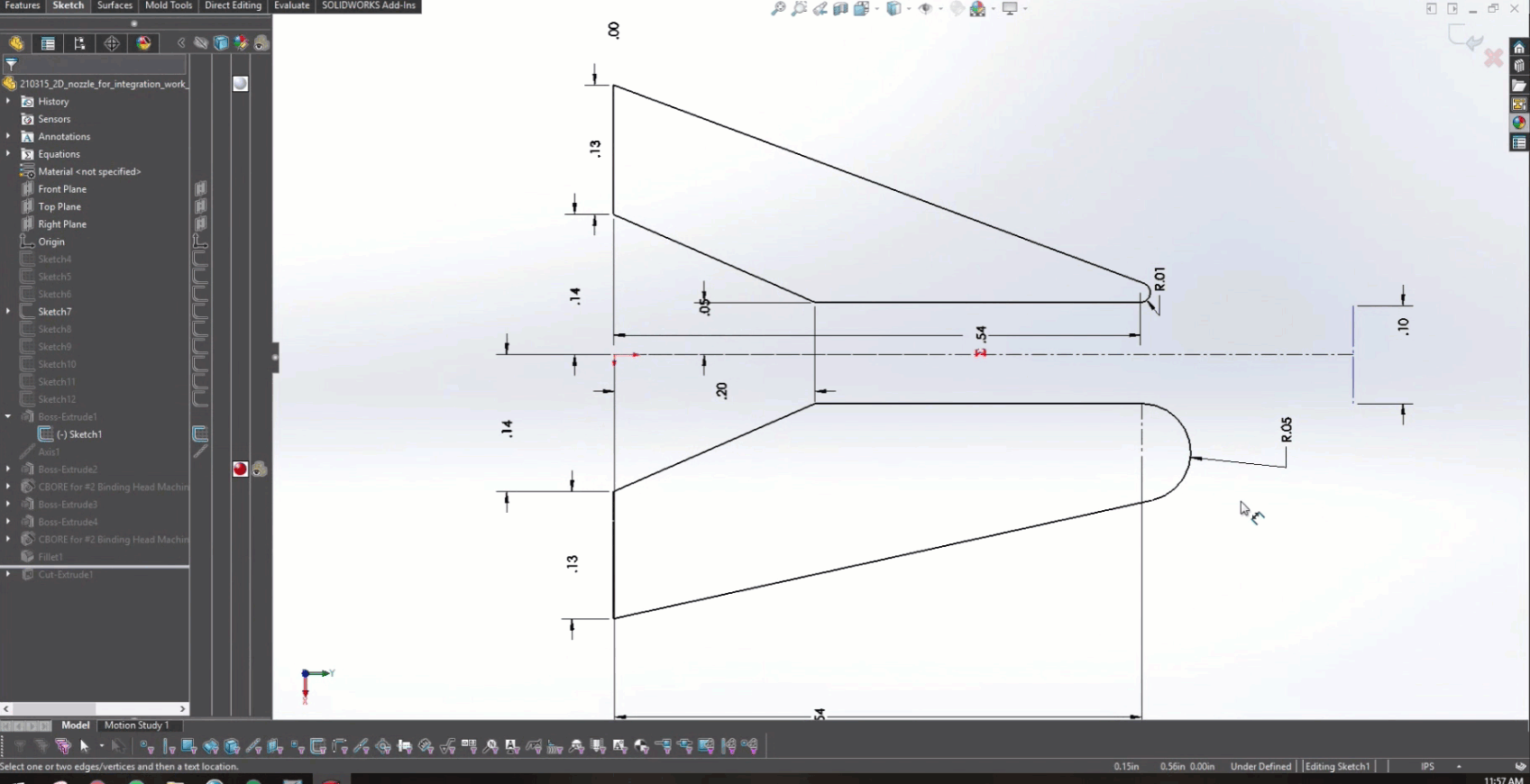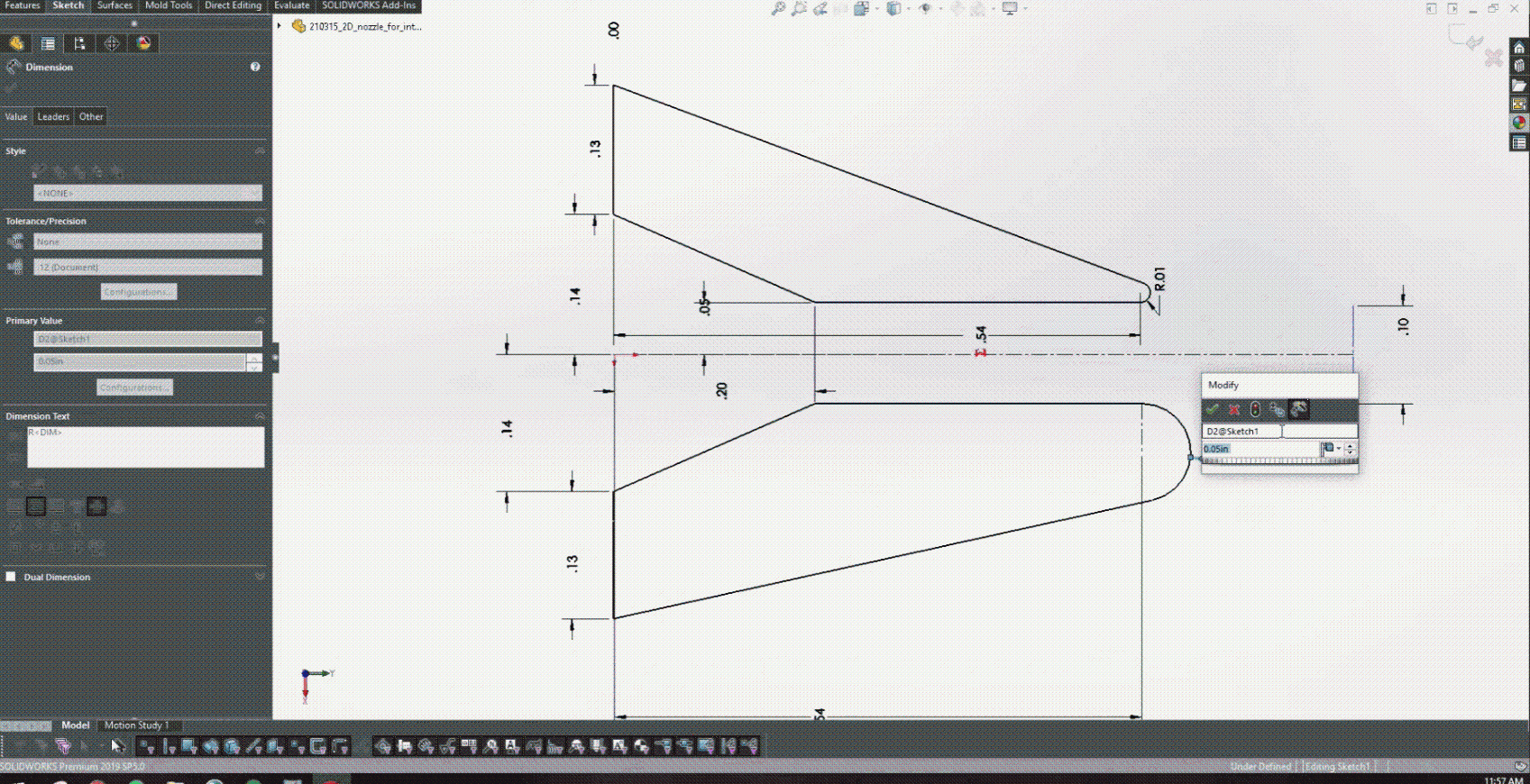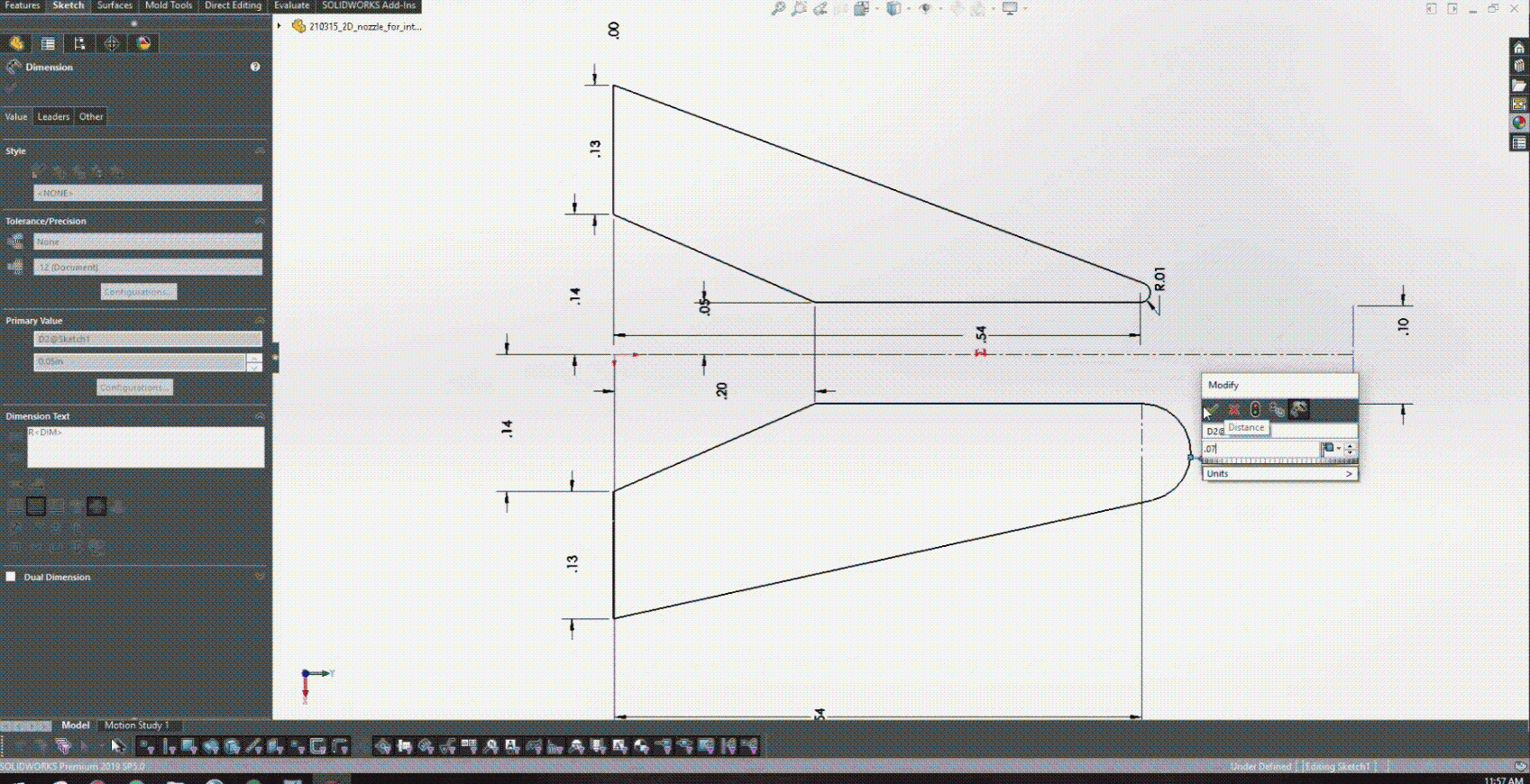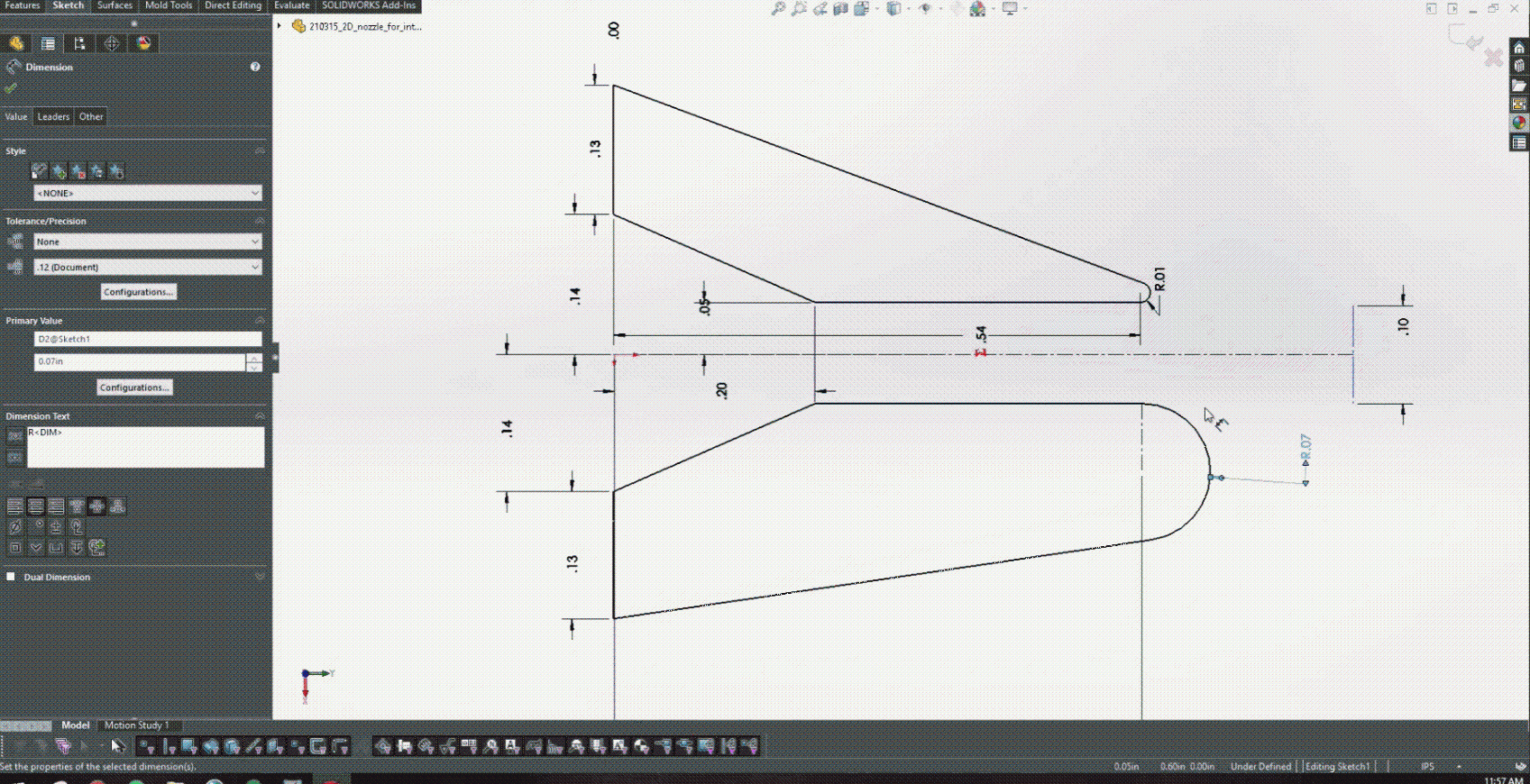
在這項工作中，氣體擦拭過程的物理簡化為二維等溫層流射流。控制此類層流射流的方程式如下：
\begin{equation} \label{eq:1}
\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0
\end{equation}
\begin{equation} \label{eq:2}
u \frac{\partial u}{\partial x} + v \frac{\partial v}{\partial y} = \nu \frac{\partial^2 u}{\partial y^2}
\end{equation}
方程 1 和 2 分別是二維層流射流的質量守恒和動量守恒，其中
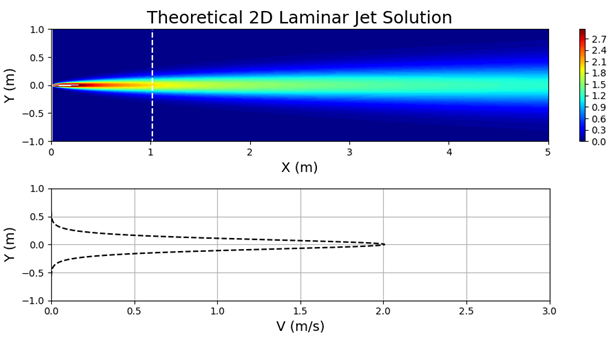
方程 1 和 2 的解可通過產生以下形式解的相似技術進行：
\begin{equation} \label{eq:3}
u = \left(\frac{3M^2}{32\rho^2\nu x}\right)^{1/3}\sech^2\left[y\left(\frac{M}{48\rho\nu^2x^2}\right)^{1/3}\right]
\end{equation}
圖 7 顯示了為指定值繪制的方程式 3
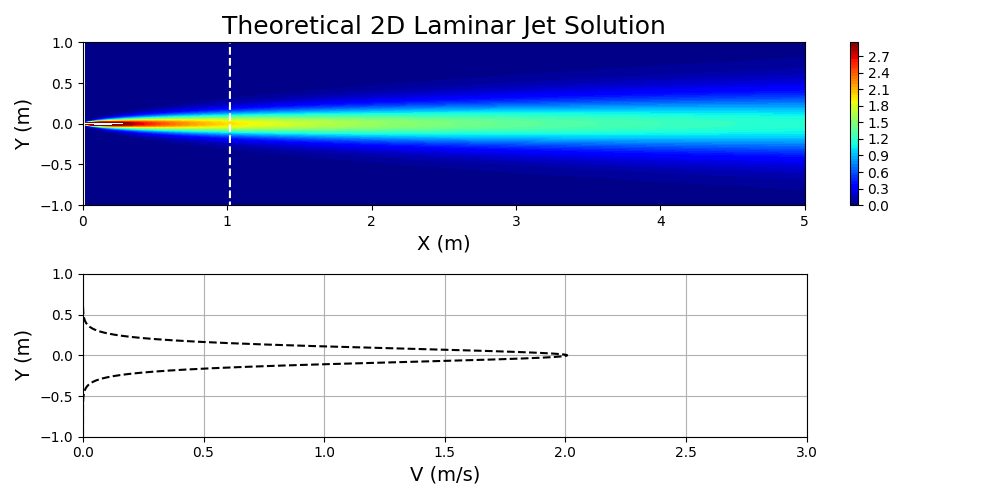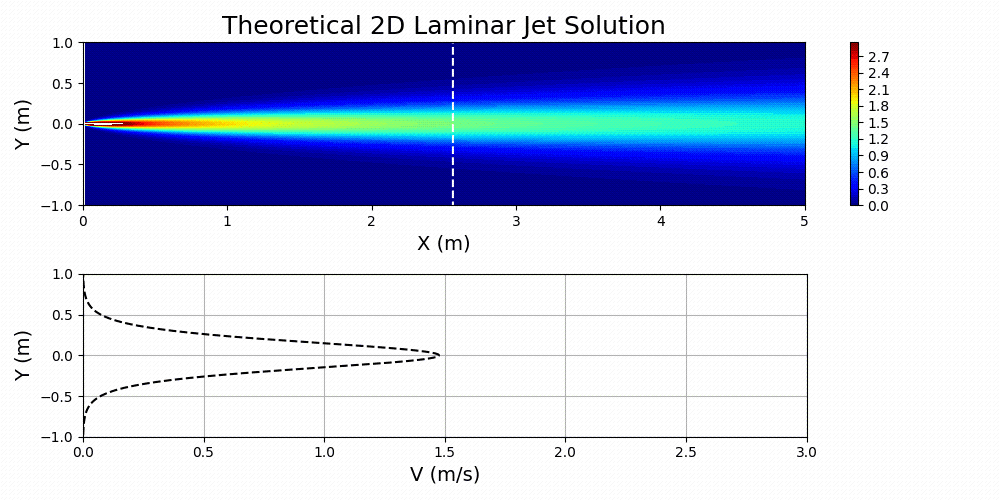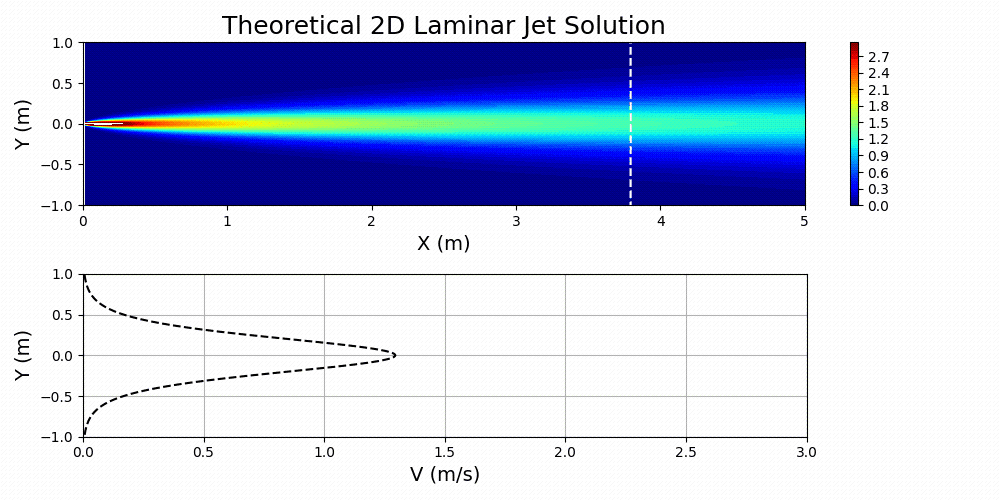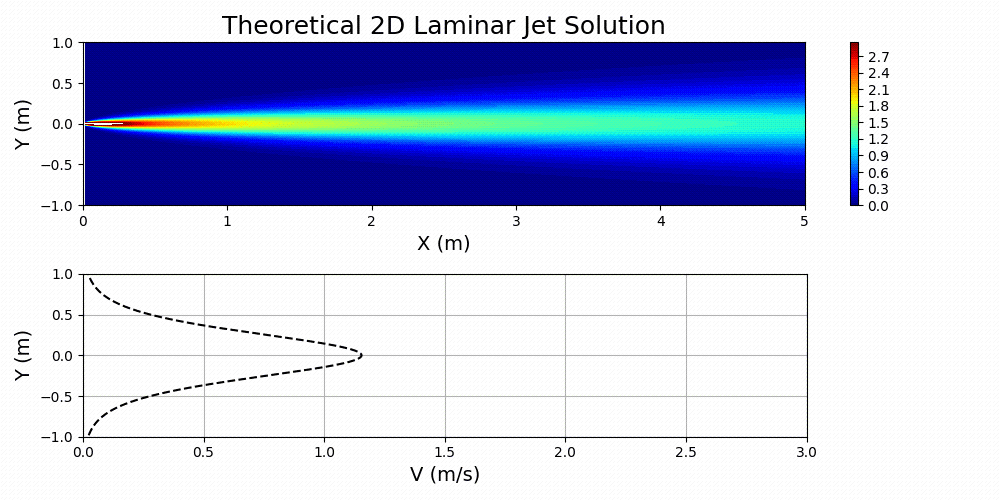
對這個問題感興趣的流體被認為是空氣。通過首先計算問題所需的雷諾數，然后基于已歸一化的域求解有效運動粘度，在主 SimNet 輸入文件中指定流體的特性。本質上，物理域和歸一化域之間的動態相似性是通過雷諾數匹配實現的：
\begin{equation} \label{eq:4}
Re = \frac{UD}{\nu} = \frac{\tilde{U}\tilde{D}}{\tilde{\nu}}
\end{equation}
使用方程式 4 ，可以指定物理速度
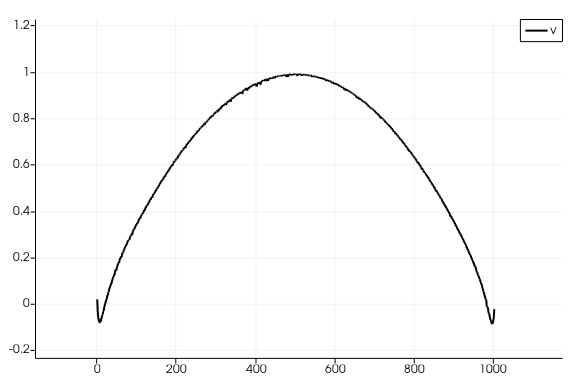
在該區域的入口處，指定了拋物線速度剖面，以防止無滑移條件緊鄰指定入口速度的墻壁附近出現任何不必要的數值剛度。因此，需要一個拋物線剖面，當它接近墻壁時，速度達到 0 （圖 8 ）。
訓練該模型所采用的數值方法是使用自適應矩估計（ Adam ）優化器，并依賴于改進的傅里葉結構。根據 SimNet 文檔中提供的指導，并通過與 NVIDIA SimNet 開發人員的合作，選擇了改進的傅立葉體系結構。
一般來說，一組守恒定律可以寫成如下：
\begin{equation} \label{eq:5}
u_t + \mathcal{N}[u] = 0, x \in \Omega, t \in [0,T]
\end{equation}
在這里
\begin{equation} \label{eq:6}
L_{residual} = \frac{1}{N_u}\sum_{i=1}^{N_u}|u(t_u^i,x_u^i)-u^i|^2 + \frac{1}{N_f}\sum_{i=1}^{N_f}|f(t_f^i,x_f^i)|^2
\end{equation}
圖 9 顯示了本工作中討論的 2D 噴嘴問題的最小化該殘余的結果。通過運行 TensorBoard ， SimNet 情況下很容易生成這種類型的損失函數殘差圖。有關此工具的更多信息，請參閱SimNet 用戶指南.
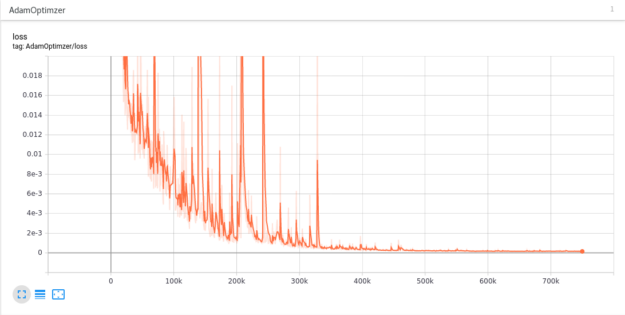
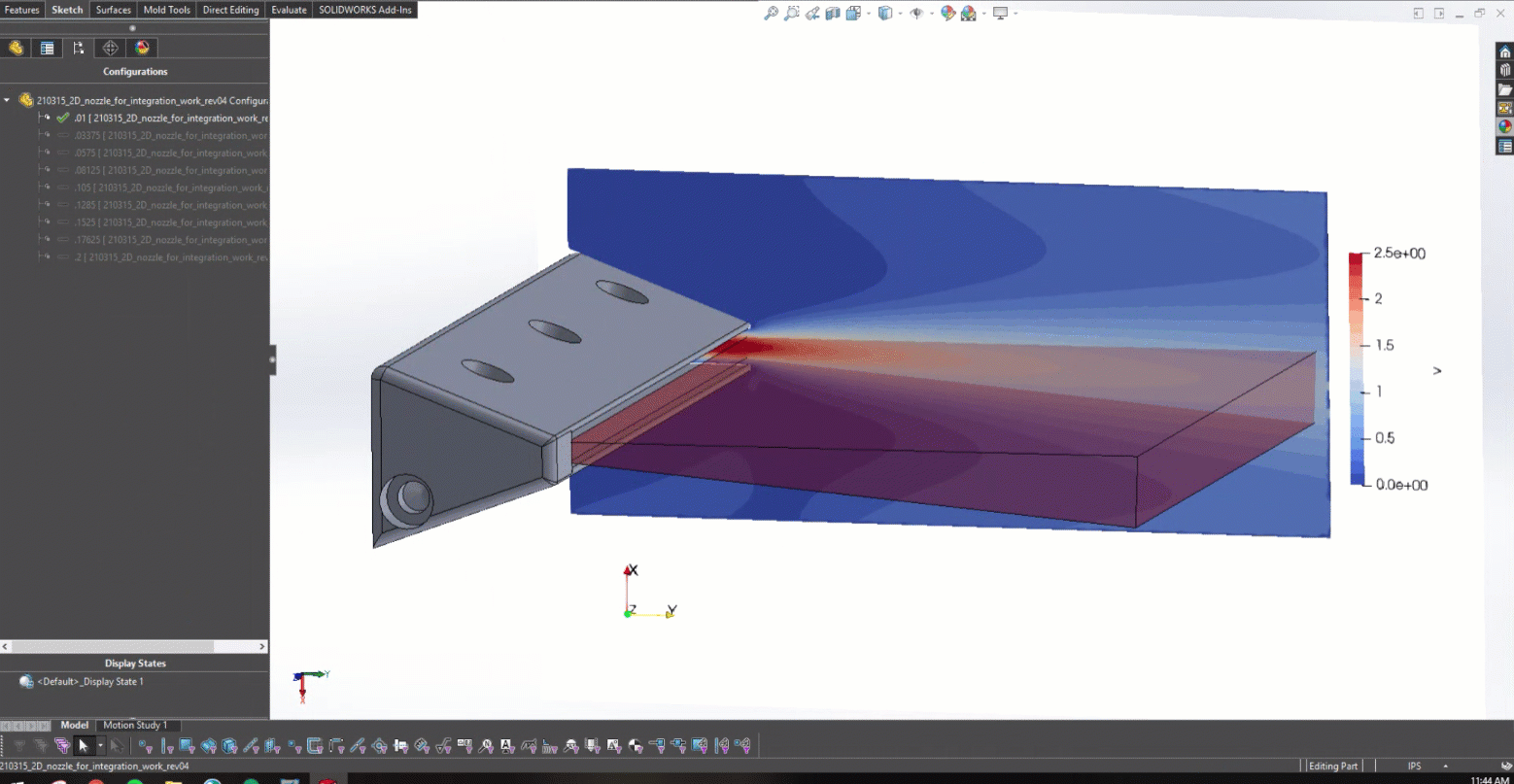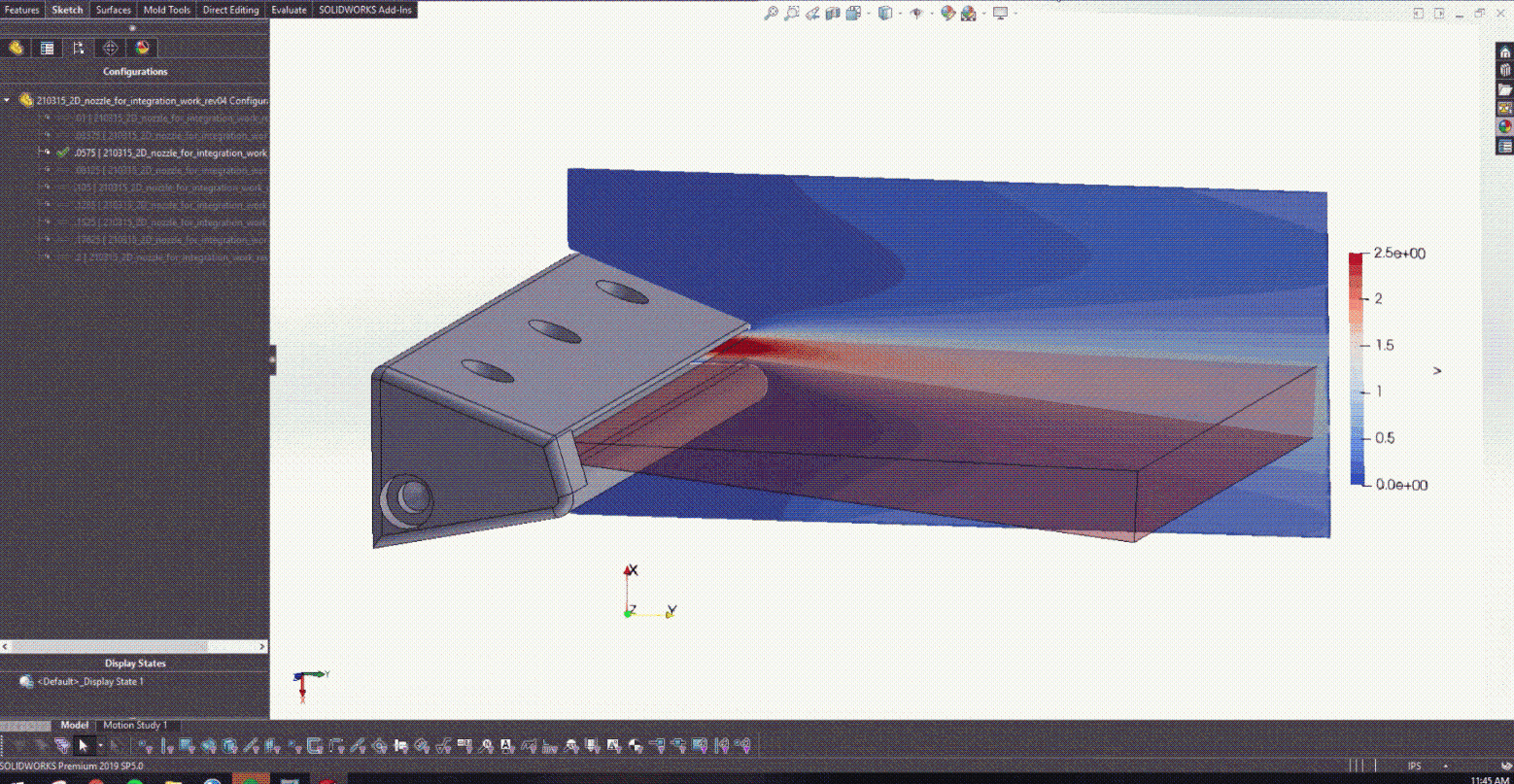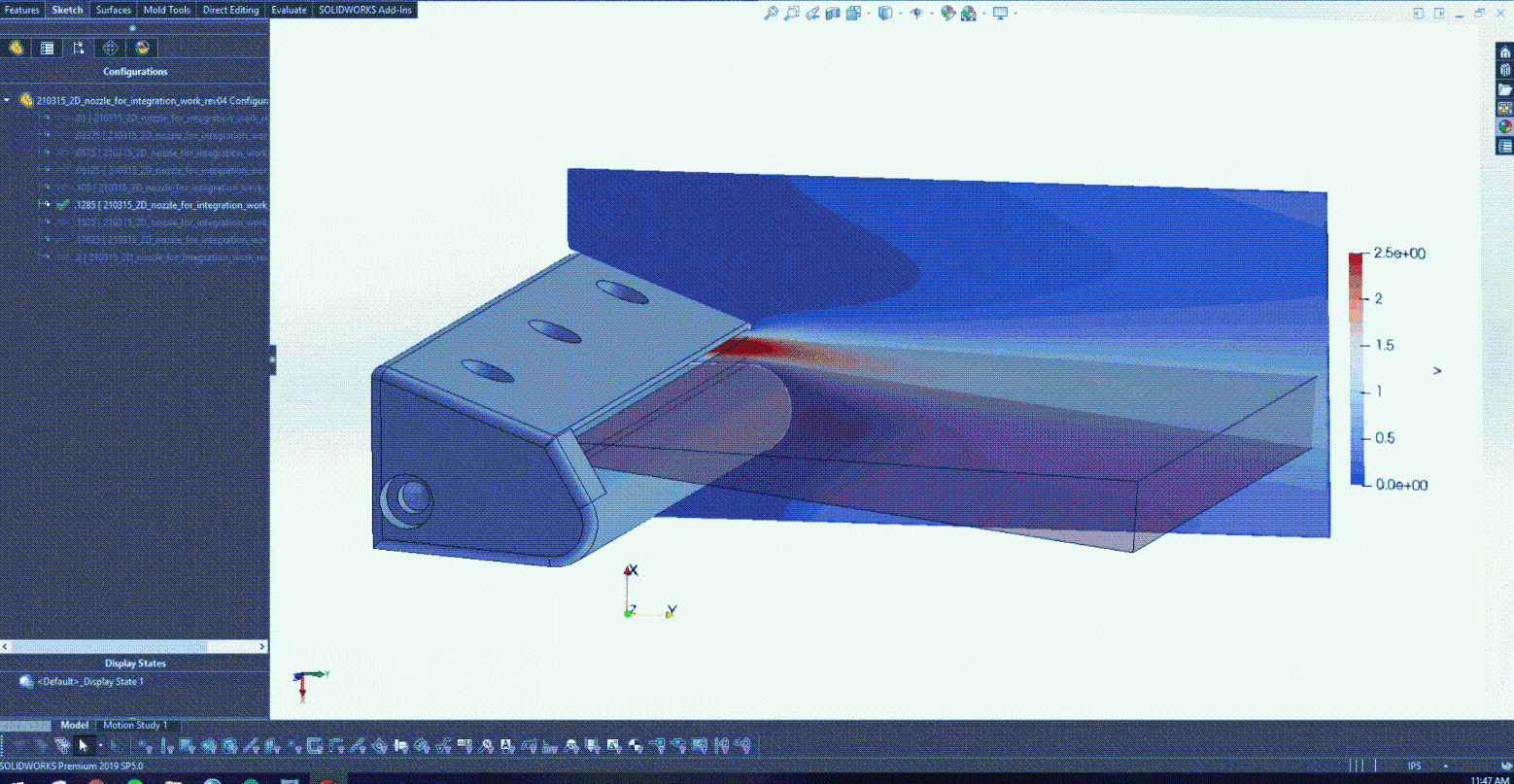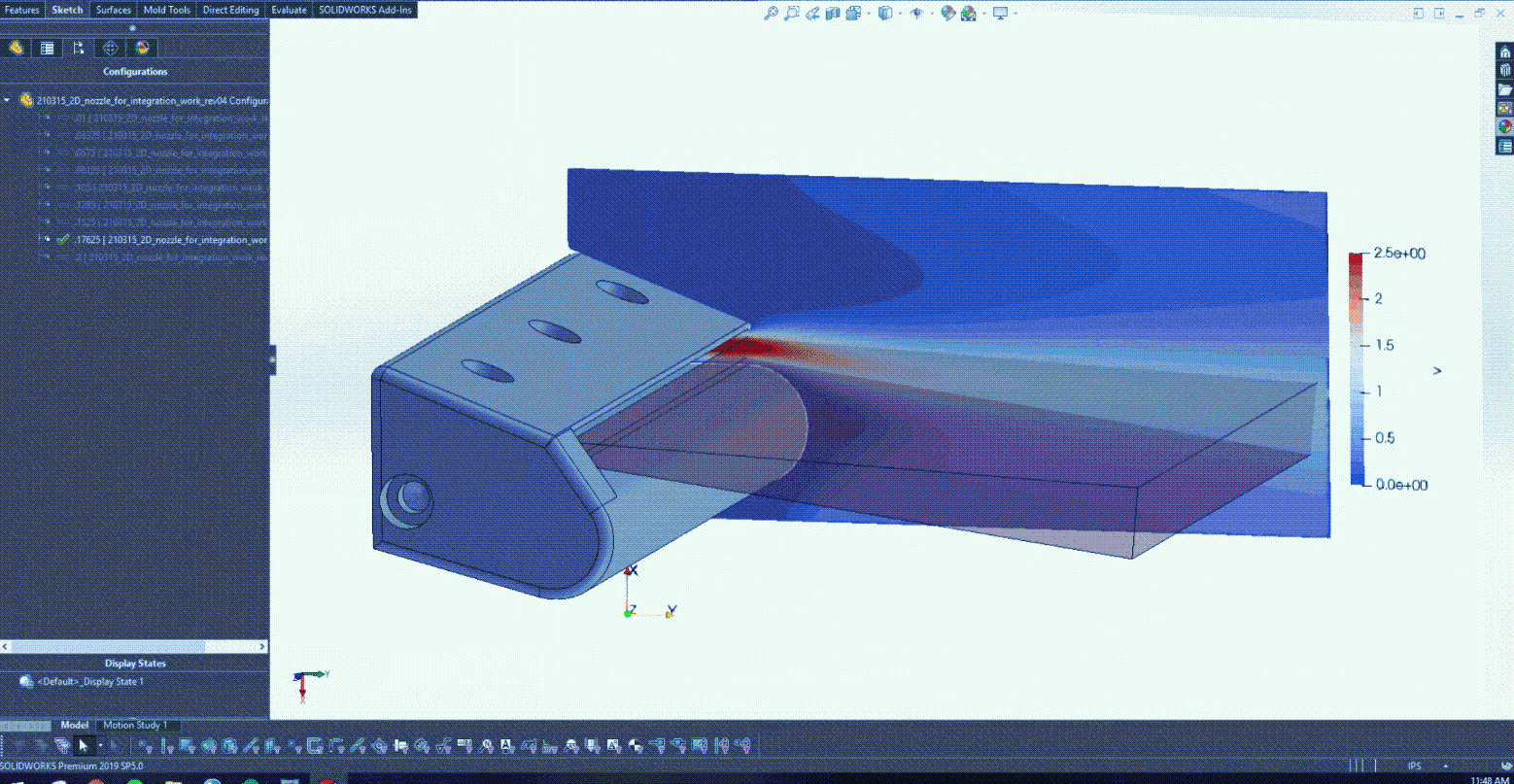
圖 10 顯示了本研究中探索的半徑子集的速度分布結果。該動畫捕捉了 SimNet 作為探索性設計工具的強大功能，可用于在大型設計空間中同時訓練釘。
結論
Michael 的應用程序目前是用 Python 編寫的概念驗證，并使用其內部 GPU 集群（ NVIDIA V100 和 NVIDIA A100 ）在一個、四個和八個 GPU 上運行。
Michael 的團隊在 SimNet 和傳統計算物理工具之間觀察到的主要區別因素是，它不依賴網格來離散域，其幾何模塊提供了構建參數化特征的靈活性，例如邊半徑。代碼在多個 GPU 上的可伸縮性是 Kinetic Vision 團隊成功證明 SimNet 是可行的產品設計工具的另一個因素。
Michael 進一步闡述了他在 SimNet 方面的經驗：
“ SimNet 代表了模擬某些類別問題的范例變化。可擴展計算可用于探索復雜問題的整個設計空間，節省數百小時的交互式工程時間以找到最佳結果。我們有許多客戶對物理建模、機器學習和 SimNet i 感興趣現在，我們已經將其列入了應對《財富》 500 強制造業挑戰的技術清單。”
有關更多信息，請參閱利用物理信息神經網絡和 SimNet 加速產品開發GTC 會議。有關功能和下載工具包的更多信息，請參閱英偉達 SimNet產品頁面。
?
