In the era of generative AI, utilizing GPUs to their maximum potential is essential to training better models and serving users at scale. Often, these models have layers that cannot be expressed as off-the-shelf library operations due to subtle modifications, and DL compilers typically forgo the last few percentage points of optimizations to make their deployment feasible.

To provide NVIDIA CUDA developers with the level of power and control needed for maximizing the performance of DL and HPC kernels, we’ve been building and iterating on CUTLASS since 2017.

It is now entering the next phase of development with a new Python interface. The fundamental abstractions introduced with the CUTLASS 3.x redesign are exposed directly in Python with CUTLASS 4.0. In this post, we discussed the design principles underlying CUTLASS 3.x, its core backend library, CUDA Tensors and Spatial Microkernels (CuTe), and optimization examples leveraging CuTe’s key features.

Highlights from CUTLASS 3.x

CUTLASS 3 introduced CuTe, a new library premised on the layout concept as a uniform and composable abstraction for describing and manipulating threads and data. By elevating layouts to a first-class citizen of the programming model, usage of CuTe greatly simplifies thread-data organization. CuTe reveals indexing logic to developers in an understandable and statically checkable way, while retaining the same high level of performance and Tensor Core operation coverage as in CUTLASS 2.x.

Beyond this more meaningful approach to layouts, CUTLASS 3 shares the same goals as all prior versions of CUTLASS — to help CUDA developers author high-performance GPU linear algebra kernels by developing an intuitive programming model around the latest hardware features. With this new major iteration, we emphasized the following:

The ability to customize any layer in the design of the library while preserving composability with other layers for developer productivity and cleaner separation of moving parts
Compile-time checks to ensure the correctness of kernel constructions. This guarantees that if it compiles, it will run correctly, with actionable static assert messages otherwise.
Reduce API surface area with fewer named types and a flatter learning curve with single points of entry that are also customization hooks.
Great performance on NVIDIA Hopper H100 and NVIDIA Blackwell B200 to use features such as WGMMA (for Hopper) or UMMA (for Blackwell), Tensor Memory Accelerator for Hopper (TMA), and threadblock clusters.

CuTe

At the heart of CUTLASS 3.x is CuTe, a new library to describe and manipulate tensors of threads and data. CuTe is made of two parts: a powerful layout representation and an algebra of operations acting on those layouts.

CuTe’s layout representation is natively hierarchical, naturally supports static and dynamic information, and is used to represent multidimensional tensors. The same layout representation is used to describe tensors of data and tensors of threads. Using the same vocabulary type across multiple independent resources shows the broad applicability of the CuTe Layout concept.

Building on this representational power, CuTe provides a formalized algebra of layouts that enable users to build complicated layouts from simple known layouts or to partition one layout across another layout. This lets programmers focus on the logical descriptions of their algorithms while CuTe does the mechanical bookkeeping for them. With these tools, users can quickly design, implement, and modify dense linear algebra algorithms.

Unlike any previous GPU programming model, the functional composition of threads and data tensors eliminates one of the most complex hurdles in GPU programming, which is that of consistently mapping a large set of threads to the data they operate upon. Once thread layouts have been described independently of the layouts of data they’ll be operating on, CuTe’s layout algebra can partition data across threads instead of having to hand implement complicated post-partitioned iteration schemes.?

CuTe layouts and tensors

More CuTe documentation on layouts and tensors can be found in its dedicated documentation directory.

CuTe provides Layout and Tensor objects that compactly package the type, shape, memory space, and layout of data, while performing the complicated indexing for the user.

Layout<Shape,Stride> provides a map between logical coordinates within Shape and indices computed with Stride. (See Figure 1 as an example)
- Shape defines one or more coordinate spaces and maps between them.
- Stride defines the index map that converts coordinates to indices.
Tensor<Engine,Layout> provides the composition of a Layout with an iterator. The iterator may be a pointer to data in global memory, shared memory, register memory, or anything else that provides random access offset and dereference.

A diagram of gray and white boxes containing logical coordinate number values showing a simplified method of manipulating them hierarchically. — *Figure 1. Multiple matrix types that can be manipulated by `Shape` and `Stride` functions to create indexes*

It’s worth highlighting that layouts in CuTe are hierarchical and inspired by folding tensor operations in tensor algebra. As shown in the figure, the hierarchical Shape and Stride enable representations of layouts that go far beyond simple row-major and column-major. At the same time, hierarchical layouts can still be accessed just like a normal tensor (e.g., the logical 2-D coordinate shown), so these more advanced data layouts are abstracted over in algorithmic development.

CuTe in CUTLASS 3.x

CUTLASS 3.x uses a single vocabulary type (cute::Layout), resulting in a simplified, formalized, and uniform layout representation to help users write extremely fast kernels with great ease.

A list of matrix math functions from CUTLASS 2.x being consolidated into a single function in CUTLASS 3.x. — *Figure 2. Shows how CUTLASS functions are simplified into a single vocabulary type call*

CuTe layouts to transform and partition

CuTe Layouts support functional composition as a core operation. Functional composition can be used to transform the shape and order of another layout. If we have a layout of data with coordinates (m,n) and we want to use coordinates (thread_idx,value_idx) instead, then we compose the data layout with a layout that describes the mapping (thread_idx,value_idx) -> (m,n).?

The result is a layout of data with coordinates (thread_idx,value_idx), which we can use to access each value of each thread very easily!

As an example, consider a 4×8 layout of data. Further, suppose that we want to assign threads and values to each coordinate of that 4×8 data. We write a “TV layout” that records the particular partitioning pattern, then perform a functional composition between the data layout and the TV layout.?

Three 2-dimensional matrices to show the mapping of 4x8 data into two other 4x8 matrices with assigned threads and values to help locate and identify the original data. — *Figure 3. An example of how a 4×8 layout of data can be assigned a thread and value pair to help coordinate access to the 4×8 data. This is known as a “TV layout”*

As shown, the composition permutes and reshapes the data such that each thread’s values are arranged across each row of the result. Simply slicing the result with our thread index completes the partitioning.

A more intuitive view of the partitioning pattern is the inverse of the TV layout.

A colorful 4x8 matrix showing the data mapping into threads and value numbers to show they have been indexed. — *Figure 4. Another 4×8 matrix representing how the original data can be mapped, the inverse of the TV layout*

This layout shows the map from each coordinate within the 4×8 data layout to the thread and value. Arbitrary partitioning patterns can be recorded and applied to arbitrary data layouts.

Additional documentation on CuTe Layout Algebra can be found on GitHub.

CuTe matrix multiply-accumulate atoms

An atom is the smallest collection of threads and data that must cooperatively participate in the execution of a hardware-accelerated math or copy operation.

An Atom combines a PTX instruction with metadata about the shape and arrangement of threads and values that must participate in that instruction. This metadata is expressed as CuTe TV layouts that can then be used to partition arbitrary tensors of input and output data. A user should in general, not have to extend this layer, as we’ll provide implementations of CuTe atoms for new architectures.

The image shows a list of programming instructions and the resulting matrix representation of MMA_Traits metadata in different colors per box. — *Figure 5. The SM70_8x8x4_F32F16F16F32_NT instruction and its associated MMA_Traits metadata*

The above image shows the SM70_8x8x4_F32F16F16F32_NT instruction and its associated MMA_Traits metadata. On the left, the TV layouts mapping (thread_id,value_id) -> coord are recorded in the traits, and on the right, the traits are visualized with the inverse coord -> (thread_id,value_id) mapping. The image on the right can be generated with

print_latex(make_tiled_mma(cute::SM70_8x8x4_F32F16F16F32_NT{}))

Additional CuTe documentation on matrix multiply-accumulate (MMA) atoms is on GitHub.

CuTe tiled MMAs

Tiled MMA and tiled copy are tilings of MMA atoms and copy atoms, respectively. We call this level “tiled” because it builds larger operations on top of the atoms as if fitting together individual tiles to build a reusable component of a mosaic. The tilings reproduce atoms across threads and data, with possible permutations and interleaving of the atoms as well.

This layer is most analogous to the warp-level tiling of MMA instructions in CUTLASS 2.x; however, it views the tiling from the perspective of all threads participating in the operation and generalizes the concept to copy operations as well. The purpose of this layer is to build composable GPU micro-kernels out of a plethora of hardware-accelerated math and data movement operations, each potentially with their own intrinsic layouts of threads and data. The tiled MMA and tiled Copy types present all these various hardware-accelerated CuTe atoms with a single, consistent API for partitioning data.

For example, CuTe might provide an MMA atom that users can call on a single warp, for fixed M, N, and K dimensions. We can then use CuTe operations make_tiled_mma to turn this atom into an operation that works on an entire thread block, for larger M, N, and K dimensions. We’ve already seen one example of a Tiled MMA in the previous section, the 1x1x1 tiling of SM70_8x8x4_F32F16F16F32_NT.

Two large multicolored matrices with thread and value indices representing individual tiles. — *Figure 6. The above image shows two more tiled MMAs using the same SM70_8x8x4_F32F16F16F32_NT atom*

This image shows two more tiled MMAs using the same SM70_8x8x4_F32F16F16F32_NT atom. On the left, four of these atoms are combined in a 2×2 row-major layout to produce a one-warp 16x16x4 MMA. On the right, four of these atoms are 2×2 row-major layouts to produce a one-warp 16x16x4 MMA, and then the rows (M) and the columns (N) are permuted to interleave the atoms. Both of these produce partitioning patterns that can be applied to any data layout, as demonstrated in the following section.

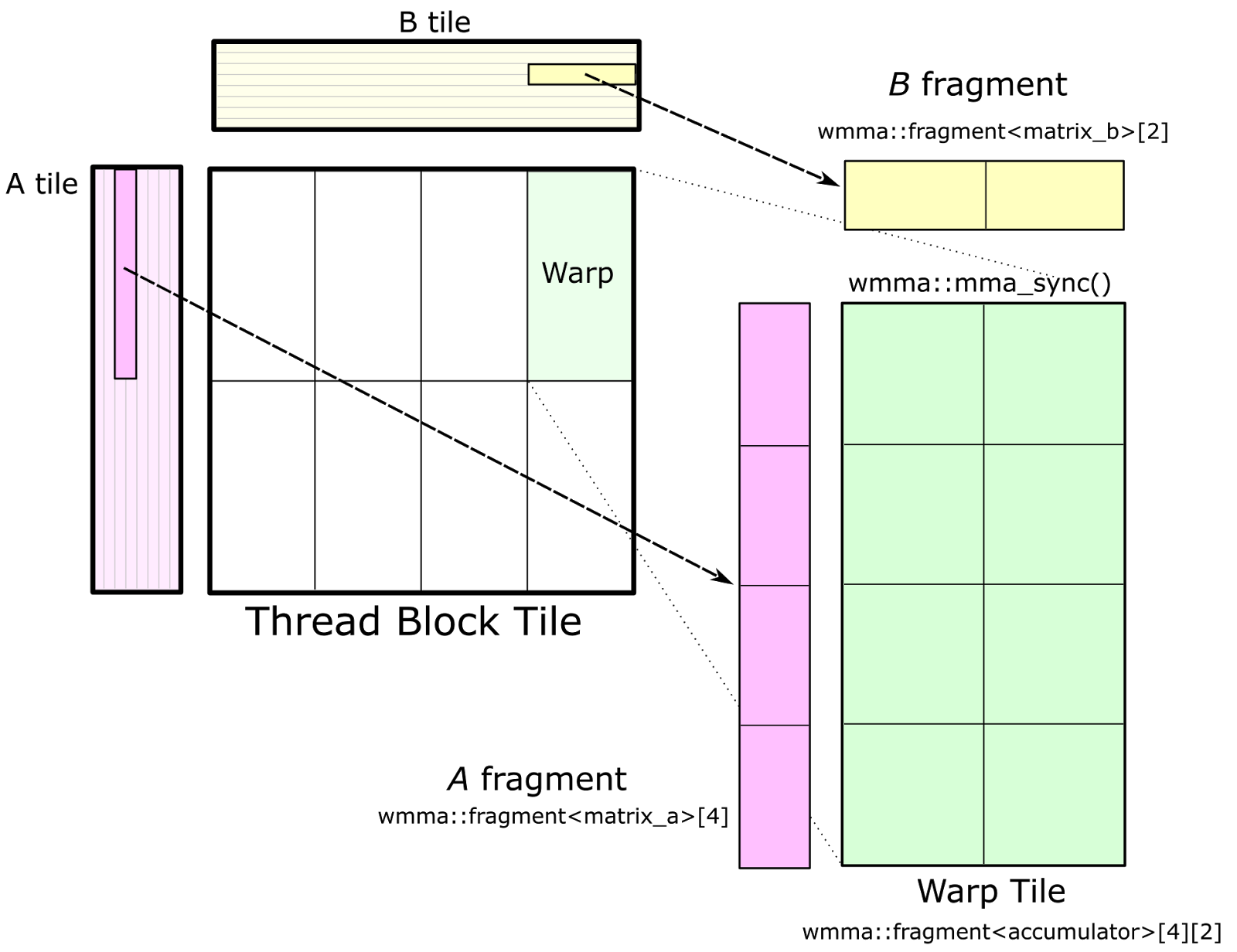
CuTe GEMMs and mainloops

With the architecture agnostic tiled API, users can build a consistent interface to GEMM outer loops, with inner loops from the atom layer.

Tensor gA = . . . // Tile of 64x16 gmem for A
Tensor gB = . . . // Tile of 96x16 gmem for B
Tensor gC = . . . // Tile of 64x96 gmem for C

// 64x16 static-layout padded row-major smem for A
Tensor sA = make_tensor(make_smem_ptr<TA>(smemAptr),
                        Layout<Shape <    _64,_16>,
                               Stride<Int<17>, _1>>{});
// 96x16 static-layout interleaved col-major smem for B
Tensor sB = make_tensor(make_smem_ptr<TB>(smemBptr),
                        Layout<Shape <Shape <_32,  _3>,_16>,
                               Stride<Stride< _1,_512>,_32>>{});

// Partition tensors across threads according to the TiledMMA
ThrMMA thr_mma = tiled_mma.get_slice(thread_idx);
Tensor tCsA = thr_mma.partition_A(sA);        // (MMA, MMA_M, MMA_K) smem
Tensor tCsB = thr_mma.partition_B(sB);        // (MMA, MMA_N, MMA_K) smem
Tensor tCgC = thr_mma.partition_C(gC);        // (MMA, MMA_M, MMA_N) gmem

// Make register tensors the same shape/layout as above
Tensor tCrA = thr_mma.make_fragment_A(tCsA);  // (MMA, MMA_M, MMA_K) rmem
Tensor tCrB = thr_mma.make_fragment_B(tCsB);  // (MMA, MMA_N, MMA_K) rmem
Tensor tCrC = thr_mma.make_fragment_C(tCgC);  // (MMA, MMA_M, MMA_N) rmem

// COPY from smem to rmem thread-level partitions
cute::copy(tCsA, tCrA);
cute::copy(tCsB, tCrB);
// CLEAR rmem thread-level partition (accumulators)
cute::clear(tCrC);

// GEMM on rmem: (V,M,K) x (V,N,K) => (V,M,N)
cute::gemm(tiled_mma, tCrA, tCrB, tCrC);
// Equivalent to
// for(int k = 0; k < size<2>(tCrA); ++k)
//   for(int m = 0; m < size<1>(tCrC); ++m)
//     for(int n = 0; n < size<2>(tCrC); ++n)
//       tiled_mma.call(tCrA(_,m,k), tCrB(_,n,k), tCrC(_,m,n));

// AXPBY from rmem to gmem thread-level partitions
cute::axpby(alpha, tCrC, beta, tCgC);
// Equivalent to
// for(int i = 0; i < size(tCrC); ++i)
//   tCgC(i) = alpha * tCrC(i) + beta * tCgC(i)

There are now many decisions to be made for the above code regarding the temporal interleaving of compute and copy instructions

Allocate rmem as only A: (MMA,MMA_M) and B: (MMA,MMA_N) and C: (MMA,MMA_M,MMA_N) Tensors and copy to it on each k-block iteration.
Account for multiple k-tiles of gmem and copy to smem on each k-tile iteration.
Overlap the above copy stages with compute stages asynchronously.
Optimize by finding better layouts of smem that improve the access patterns for the smem -> rmem copy.
Optimize by finding efficient TiledCopy partitioning patterns for the gmem -> smem copy.

These concerns are considered part of the “temporal micro-kernels” rather than the “spatial micro-kernels” that CuTe provides. In general, decisions regarding the pipelining and execution of instructions over CuTe Tensors are left to the CUTLASS level and will be discussed in the next part of this series.

Summary

In summary, CuTe empowers developers to write more readable, maintainable, and high-performance CUDA code by abstracting away the low-level details of tensor layout and thread mapping, and providing a unified, algebraic interface for dense linear algebra on modern NVIDIA GPUs.

For more information, you can download the software on GitHub, read our documentation, or join our Developer Forum for deeper discussions.

Acknowledgments

For their contributions to this post, thanks to Jack Kosaian, Mark Hoemmen, Haicheng Wu, and Matt Nicely. Special thanks to the Colfax International team of Jay Shah, Paul VanKoughnett, and Ryo Asai.